Scott Pesme
 |
Hi there!Since October 2024, I am a post-doc in the Thoth team at Inria Grenoble, under the supervision of Julien Mairal. Prior to that, from September 2019 to June 2024, I was a PhD student at EPFL in the Theory of Machine Learning group and advised by Nicolas Flammarion. My PhD thesis is entitled “Deep Learning Theory Through the Lens of Diagonal Linear Networks” and you can find the manuscript here. Contact
|
My research motivations in words
I tell my bohemian friends that I do math, and I avoid mentioning the “AI” part. When they ask for more details, I say that I am a neuroscientist for intelligent computers and I try to convince them it's pretty fascinating (and that I'm not actively destroying the planet).
In practice, my work focuses on understanding why neural networks are so good at what they do. How is it that we can train them using gradient-based methods? Why do these trained networks generalise so well to new data? How, and why, does a neural network make a certain decision? And so on.
 |
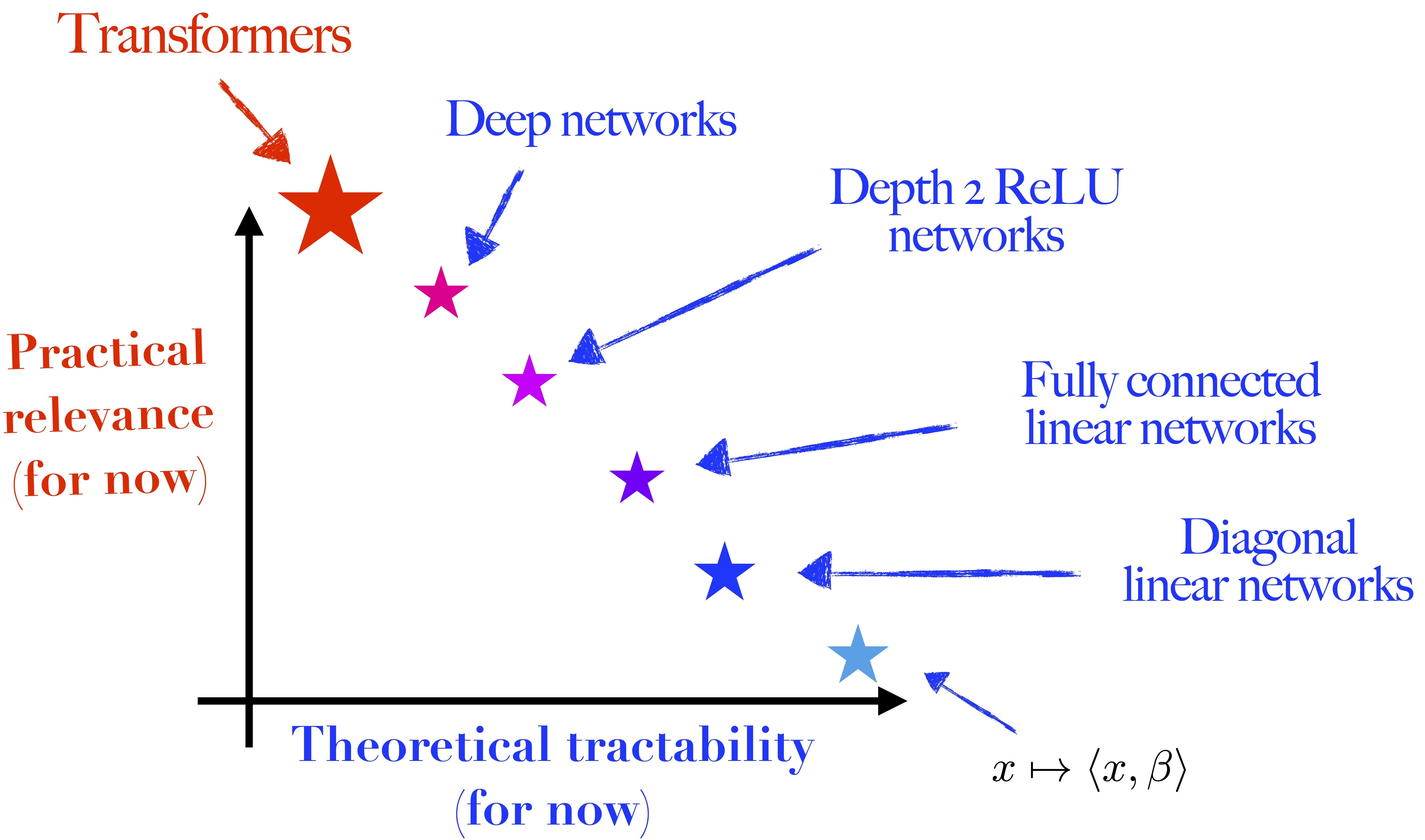To tackle these questions, even though I feel my approach is closer to that of a physicist, my main toolbox is mathematics. I use tools from optimisation, statistics, ordinary and stochastic differential equation theory, probability theory, etc. As we cannot understand complex systems if we cannot explain the simpler ones, my aim is to adopt a bottom-up approach, starting with the simplest (yet not fully understood) neural network architectures and progressively building from there. The hope is that each step of increasing complexity will develop an understanding and intuition that can help unlock the next. Ultimately, the goal being to understand settings that are practically relevant and of real-world use. Following this approach, I mainly focused on diagonal linear networks during my PhD. |
My research interests in a picture
 |
Publications (and other)
If you want a friendly introduction to the concept of implicit bias, I would recommend having a look at the blogpost that Loucas kindly proposed me to write with him for Francis Bach's blog, you can also have a look at Chapter 2 in my PhD manuscript. And if you want an introduction to this architecture, you can have a look at Chapter 3 in my PhD manuscript. If you are interested in the content of one of the papers, I would recommend having a look at the Bluesky thread (or at the blogpost for the Neurips 2021 paper) before reading the paper. I like these formats as they allow to explain things in a (hopefully) more friendly way!
E. Boursier, S. Pesme, R-A. Dragomir. A Theoretical Framework for Grokking: Interpolation followed by Riemannian Norm Minimisation.
[arxiv, pdf]. [Show Abstract]Abstract: We study the dynamics of gradient flow with small weight decay on general training losses $F: \mathbb{R}^d to \mathbb{R}$. Under mild regularity assumptions and assuming convergence of the unregularised gradient flow, we show that the trajectory with weight decay $\lambda$ exhibits a two-phase behaviour as $\lambda \to 0$. During the initial fast phase, the trajectory follows the unregularised gradient flow and converges to a manifold of critical points of $F$. Then, at time of order $1/\lambda$, the trajectory enters a slow drift phase and follows a Riemannian gradient flow minimising the $\ell_2$-norm of the parameters. This purely optimisation-based phenomenon offers a natural explanation for the grokking effect observed in deep learning, where the training loss rapidly reaches zero while the test loss plateaus for an extended period before suddenly improving. We argue that this generalisation jump can be attributed to the slow norm reduction induced by weight decay, as explained by our analysis. We validate this mechanism empirically on several synthetic regression tasks.
S. Pesme, R-A. Dragomir, N. Flammarion. Implicit Bias of Mirror Flow on Separable Data.
[poster, arxiv, pdf], NeurIPS 2024. [Show Abstract]Abstract: We examine the continuous-time counterpart of mirror descent, namely mirror flow, on classification problems which are linearly separable. Such problems are minimised ‘at infinity’ and have many possible solutions; we study which solution is preferred by the algorithm depending on the mirror potential. For exponential tailed losses and under mild assumptions on the potential, we show that the iterates converge in direction towards a $\phi_\infty$-maximum margin classifier. The function $\phi_\infty$ is the ‘horizon function’ of the mirror potential and characterises its shape ‘at infinity’. When the potential is separable, a simple formula allows to compute this function. We analyse several examples of potentials and provide numerical experiments highlighting our results.
H. Papazov, S. Pesme, N. Flammarion. Leveraging Continuous Time to Understand Momentum When Training Diagonal Linear Networks.
[poster, arxiv, pdf], AISTATS 2024. [Show Abstract]Abstract: In this work, we investigate the effect of momentum on the optimisation trajectory of gradient descent. We leverage a continuous-time approach in the analysis of momentum gradient descent with step size $\gamma$ and momentum parameter $\beta$ that allows us to identify an intrinsic quantity $\lambda = \gamma /(1 - \beta)^2 $ which uniquely defines the optimisation path and provides a simple acceleration rule. When training a $2$-layer diagonal linear network in an overparametrised regression setting, we characterise the recovered solution through an implicit regularisation problem. We then prove that small values of $\lambda$ help to recover sparse solutions. Finally, we give similar but weaker results for stochastic momentum gradient descent. We provide numerical experiments which support our claims.
S. Pesme, N. Flammarion. Saddle-to-Saddle Dynamics in Diagonal Linear Networks.
[poster, (not a twitter) thread, arxiv, pdf], NeurIPS 2023. [Show Abstract]Abstract: In this paper we fully describe the trajectory of gradient flow over diagonal linear networks in the limit of vanishing initialisation. We show that the limiting flow successively jumps from a saddle of the training loss to another until reaching the minimum $\ell_1$-norm solution. This saddle-to-saddle dynamics translates to an incremental learning process as each saddle corresponds to the minimiser of the loss constrained to an active set outside of which the coordinates must be zero. We explicitly characterise the visited saddles as well as the jumping times through a recursive algorithm reminiscent of the Homotopy algorithm used for computing the Lasso path. Our proof leverages a convenient arc-length time-reparametrisation which enables to keep track of the heteroclinic transitions between the jumps. Our analysis requires negligible assumptions on the data, applies to both under and overparametrised settings and covers complex cases where there is no monotonicity of the number of active coordinates. We provide numerical experiments to support our findings.
M. Even, S. Pesme, S. Gunasekar, N. Flammarion. (S)GD over Diagonal Linear Networks: Implicit Regularisation, Large Stepsizes and Edge of Stability.
[poster, (not a twitter) thread, arxiv, pdf], NeurIPS 2023. [Show Abstract]Abstract: In this paper, we investigate the impact of stochasticity and large stepsizes on the implicit regularisation of gradient descent (GD) and stochastic gradient descent (SGD) over diagonal linear networks. We prove the convergence of GD and SGD with macroscopic stepsizes in an overparametrised regression setting and characterise their solutions through an implicit regularisation problem. Our crisp characterisation leads to qualitative insights about the impact of stochasticity and stepsizes on the recovered solution. Specifically, we show that large stepsizes consistently benefit SGD for sparse regression problems, while they can hinder the recovery of sparse solutions for GD. These effects are magnified for stepsizes in a tight window just below the divergence threshold, in the “edge of stability” regime. Our findings are supported by experimental results.
S. Pesme, L. Pillaud-Vivien, N. Flammarion. Implicit Bias of SGD for Diagonal Linear Networks: a Provable Benefit of Stochasticity.
[poster, blogpost, slides, arxiv, pdf], NeurIPS 2021. [Show Abstract]Abstract: Understanding the implicit bias of training algorithms is of crucial importance in order to explain the success of overparametrised neural networks. In this paper, we study the dynamics of stochastic gradient descent over diagonal linear networks through its continuous time version, namely stochastic gradient flow. We explicitly characterise the solution chosen by the stochastic flow and prove that it always enjoys better generalisation properties than that of gradient flow. Quite surprisingly, we show that the convergence speed of the training loss controls the magnitude of the biasing effect: the slower the convergence, the better the bias. To fully complete our analysis, we provide convergence guarantees for the dynamics. We also give experimental results which support our theoretical claims. Our findings highlight the fact that structured noise can induce better generalisation and they help explain the greater performances observed in practice of stochastic gradient descent over gradient descent.
S. Pesme, N. Flammarion. Online Robust Regression via SGD on the l1 loss.
[poster, arxiv, pdf], NeurIPS 2020. [Show Abstract]Abstract: We consider the robust linear regression problem in the online setting where we have access to the data in a streaming manner, one data point after the other. More specifically, for a true parameter $\theta^*$, we consider the corrupted Gaussian linear model $y = \langle x, \theta^* \rangle + \varepsilon + b$ where the adversarial noise $b$ can take any value with probability $\eta$ and equals zero otherwise. We consider this adversary to be oblivious (i.e., $b$ independent of the data) since this is the only contamination model under which consistency is possible. Current algorithms rely on having the whole data at hand in order to identify and remove the outliers. In contrast, we show in this work that stochastic gradient descent on the $\ell_1$ loss converges to the true parameter vector at a $\tilde{O}(1/(1− \eta )^2 n)$ rate which is independent of the values of the contaminated measurements. Our proof relies on the elegant smoothing of the non-smooth $\ell_1$ loss by the Gaussian data and a classical non-asymptotic analysis of Polyak-Ruppert averaged SGD. In addition, we provide experimental evidence of the efficiency of this simple and highly scalable algorithm.
S. Pesme, A. Dieuleveut, N. Flammarion.On Convergence-Diagnostic based Step Sizes for Stochastic Gradient Descent.
[arxiv, pdf], ICML 2020. [Show Abstract]Abstract: Constant step-size Stochastic Gradient Descent exhibits two phases: a transient phase during which iterates make fast progress towards the optimum, followed by a stationary phase during which iterates oscillate around the optimal point. In this paper, we show that efficiently detecting this transition and appropriately decreasing the step size can lead to fast convergence rates. We analyse the classical statistical test proposed by Pflug (1983), based on the inner product between consecutive stochastic gradients. Even in the simple case where the objective function is quadratic we show that this test cannot lead to an adequate convergence diagnostic. We then propose a novel and simple statistical procedure that accurately detects stationarity and we provide experimental results showing state-of-the-art performance on synthetic and real-world datasets.
You can have a look at my Google scholar webpage or follow me to the (blue) sky!